
5.带电粒子在电场中的运动
课标要求 | 素养目标 |
1.学习运用静电力、电场强度等概念研究带电粒子在电场中受到的力和运动的关系,培养运动和相互作用观念。 2.学习运用静电力做功、电势、电势差、等势面等概念研究带电粒子在电场中的功能关系,培养能量观念。 3.了解示波管的工作原理,体会静电场知识对科学技术的影响,培养解决实际问题的能力 | 1.通过研究带电粒子在电场中的偏转学会类比的研究方法。(科学思维) 2.通过带电粒子在电场中加速、偏转过程的分析,培养学生的分析、推理能力。(科学推理) 3.观察示波管,知道其主要构造和工作原理,体会静电场知识在科学技术中的应用。(科学态度与责任) 4.通过知识的应用,培养学生运用科学知识解决实际问题的能力。(科学态度与责任) |

知识点一 带电粒子在电场中的加速
1.带电粒子的运动特点
利用 电场 使带电粒子加速,其速度方向与 电场强度 的方向相同或相反。
2.两种分析思路
(1)利用牛顿第二定律结合 匀变速直线运动 公式,适用于 匀强 电场且问题中涉及运动时间等描述运动过程的物理量时适合该思路。
(2)利用静电力做功结合 动能定理 ,当问题只涉及 位移 、速率等动能定理公式中的物理量或 非匀强 电场情景时适合该思路。
知识点二 带电粒子在电场中的偏转
1.条件:带电粒子的初速度方向跟电场方向 垂直 。
2.运动规律:在匀强电场中,带电粒子做类平抛运动,运动轨迹是一条 抛物线 。
3.分析思路:同分析平抛运动的思路相同,不同的是平抛运动物体所受的是重力,而带电粒子所受的是静电力。
4.示波管[拓展学习]
(1)构造示意图
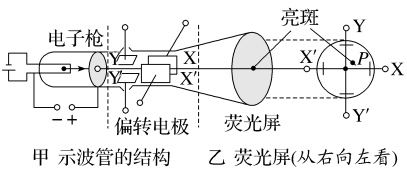
(2)原理:电子在 加速 电场中加速,在 偏转 电场中偏转后打在荧光屏上。
【情景思辨】
如图所示,一电子在加速电场中加速后进入偏转电场运动。
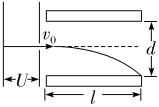
(1)忽略重力,带电粒子加速时做匀变速直线运动。( √ )
(2)若电子由静止开始加速,满足动能定理eU= m
m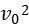 。( √ )
。( √ )
(3)电子在匀强电场中偏转时,可能做匀速圆周运动。( × )
(4)当其他条件相同时,v0越大,电子在偏转电场中偏转距离越大。( × )

要点一 带电粒子在电场中的加速

1.带电粒子的分类及受力特点
(1)微观粒子:电子、质子、α粒子、离子等基本粒子,一般都不考虑重力。
(2)质量较大的微粒:带电小球、带电油滴、带电颗粒等,除有说明或有明确的暗示外,处理问题时一般都不能忽略重力。
2.带电粒子只受静电力作用的加速问题分析
(1)加速度
由F=qE=q =ma得a=
=ma得a=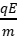 =
=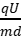 。
。
(2)速度
①利用功能关系求解(适用于所有电场)
由qU= mv2-
mv2- m
m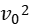 得v=
得v= 
若初速度v0=0,则v= 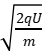 。
。
②利用力和运动关系求解(仅适用于匀强电场)
由v2=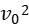 +2ad=
+2ad=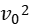 +
+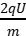 得v=
得v= 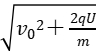
若初速度v0=0,则v= 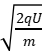 。
。
【典例1】 如图所示,在P板附近有一电子(图中未画出)由静止开始向Q板运动,则下列关于电子到达Q板时的速率与哪些因素有关的解释正确的是( )
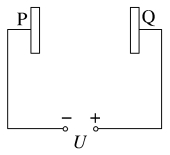
A.两极板间的距离越大,加速的时间就越长,则获得的速率越大
B.两极板间的距离越小,加速的时间就越短,则获得的速率越小
C.两极板间的距离越小,加速度就越大,则获得的速率越大
D.与两板间的距离无关,仅与加速电压U有关
答案:D
解析:电子从静止运动到Q板的过程中只有静电力做功,设电子的质量为m,电荷量为e,运动到Q板时的速率为v,根据动能定理得eU= mv2,解得v=
mv2,解得v= ,可知电子运动到Q板时的速率与两极板间的距离无关,仅与加速电压U有关,故选项D正确。
,可知电子运动到Q板时的速率与两极板间的距离无关,仅与加速电压U有关,故选项D正确。
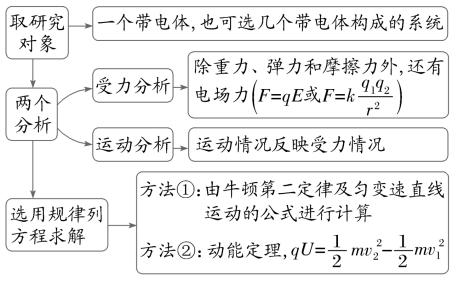
规律方法
带电粒子在电场中直线运动问题的分析方法
![]()
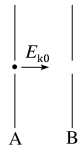
1.如图所示,A、B是一对中心有孔的圆盘,它们间有一定的电势差UAB,一电子(不计重力)以一定初动能Ek0=500 eV进入A圆盘中心,如果UAB=600 V,那么电子飞出圆盘中心的动能是Ek1;如果UAB=-600 V,那么电子射出圆盘中心的动能是Ek2,则( )
A.Ek1=1 100 eV,Ek2=500 eV
B.Ek1=500 eV,Ek2=1 100 eV
C.Ek1=-100 eV,Ek2=1 100 eV
D.Ek1=1 100 eV,Ek2=100 eV
解析:B 如果UAB=600 V,A电势高于B,电子在A、B间所受静电力方向指向A,又因为Ek0<eUAB,所以电子无法从B的小孔中射出,最终又会返回A的小孔,整个过程静电力做功为零,根据动能定理可得Ek1=Ek0=500 eV,如果UAB=-600 V,A电势低于B,电子在A、B间所受静电力方向指向B,电子将始终加速,根据动能定理可得Ek2-Ek0=-eUAB,解得Ek2=1 100 eV,故选B。
2.(2023·江苏徐州高二期末)电子被加速器加速后轰击重金属靶时,会产生射线,可用于放射治疗。图甲展示了一台医用电子直线加速器,其原理如图乙所示:从阴极射线管的阴极K发射出来的电子(速度可忽略),经电势差的绝对值为U的电场加速后获得速度v,加速电场两极板间的距离为d,不计电子所受重力。下列操作可使v增大的是( )
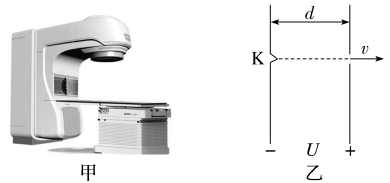
A.仅增大U B.仅减小U
C.仅增大d D.仅减小d
解析:A 电子在电场中加速,由动能定理可得eU= mv2,解得v=
mv2,解得v= ,所以可使v增大的操作是仅增大U。故A正确。
,所以可使v增大的操作是仅增大U。故A正确。
要点二 带电粒子在电场中的偏转

1.带电粒子在匀强电场中偏转的基本规律
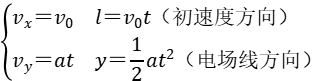
2.偏转位移和偏转角
(1)粒子离开电场时的偏转位移y= at2=
at2=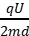 ·
·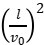 =
=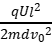 。
。
(2)粒子离开电场时的偏转角tan θ=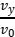 =
=![]() 。
。
(3)粒子离开电场时位移与初速度夹角的正切值tan α=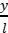 =
=![]() 。
。
3.两个常用的推论
(1)粒子射出电场时速度的反向延长线交于板长l的 处,即x=
处,即x=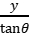 =
= 。
。
(2)位移方向与初速度方向夹角的正切值为速度偏转角正切值的 ,即tan α=
,即tan α=![]() tan θ。
tan θ。
4.运动轨迹:抛物线。
【典例2】 如图所示,电子从静止开始被U=180 V的电场加速,沿直线垂直进入另一个电场强度为E=6 000 V/m的匀强偏转电场,而后电子从右侧离开偏转电场。已知电子比荷为 ≈
≈ ×1011 C/kg,不计电子的重力,偏转极板长为L=6.0×10-2 m。求:
×1011 C/kg,不计电子的重力,偏转极板长为L=6.0×10-2 m。求:
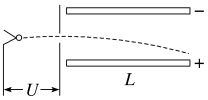
(1)电子经过电压U加速后的速度vx的大小;
(2)电子在偏转电场中运动的加速度a的大小;
(3)电子离开偏转电场时的速度方向与刚进入该电场时的速度方向之间的夹角θ。
答案:(1)8×106 m/s (2)1.1×1015 m/s2 (3)45°
解析:(1)根据动能定理可得eU= m
m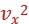 ,
,
解得vx=8×106 m/s。
(2)电子在偏转电场中受到竖直向下的静电力,
根据牛顿第二定律得a=
解得a= ×1014 m/s2≈1.1×1015 m/s2。
×1014 m/s2≈1.1×1015 m/s2。
(3)电子在水平方向上做匀速直线运动,故t=
在竖直方向上做初速度为零的匀加速直线运动,
故vy=at,tan θ=
联立解得θ=45°。

1.如图所示,静止的电子在加速电压U1的作用下从O经P板的小孔射出,又垂直进入平行金属板间的电场,在偏转电压U2的作用下偏转一段距离。现使U1加倍,要想使电子的运动轨迹不发生变化,应该( )
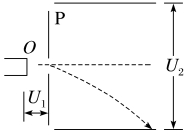
A.使U2加倍
B.使U2变为原来的4倍
C.使U2变为原来的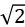 倍
倍
D.使U2变为原来的
解析:A 设偏转极板的长度为L,板间距离为d,则根据推论可知,偏转距离y=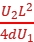 。使U1加倍,要想使电子的运动轨迹不发生变化,即y不变,则必须使U2加倍,故选A。
。使U1加倍,要想使电子的运动轨迹不发生变化,即y不变,则必须使U2加倍,故选A。
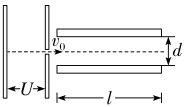
2.一束电子流经U=5 000 V的加速电压加速后,在距两平行极板等距离处垂直进入板间的匀强电场,如图所示。若两极板间距离d=1.0 cm,板长l=5.0 cm,那么要使电子能从极板间飞出,两极板间最大能加多大电压?
答案:400 V
解析:在加速过程中,由动能定理得eU= m
m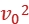
进入偏转电场后,电子在平行于极板方向上做匀速直线运动,有l=v0t
在垂直于极板方向上电子做匀加速直线运动,
加速度a= =
=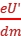
又偏移距离y= at2
at2
能从平行极板间飞出的条件为y≤
联立以上各式解得U'≤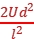 =400 V
=400 V
即要使电子能从极板间飞出,两极板间所加最大电压为400 V。
要点三 示波管的原理

电子枪通电后发射电子,电子在加速电场作用下被加速,然后进入偏转电场。偏转电极一般有相互垂直的两组,一组控制竖直偏转,一组控制水平偏转。电子经过偏转电场后打到荧光屏上使荧光粉发光。
【典例3】 如图是示波管的原理图。它由电子枪、偏转电极(XX'和YY')、荧光屏组成,管内抽成真空。给电子枪通电后,如果在偏转电极XX'和YY'上都没有加电压,电子束将打在荧光屏的中心O点,在那里产生一个亮斑。下列说法错误的是( )

A.要想让亮斑沿OY向上移动,需在偏转电极YY'上加电压,且Y'比Y电势高
B.要想让亮斑移到荧光屏的右上方,需在偏转电极XX'、YY'上加电压,且X比X'电势高、Y比Y'电势高
C.要想在荧光屏上出现一条水平亮线,需在偏转电极XX'上加特定的周期性变化的电压(扫描电压),在偏转电极YY'上加恒定电压或不加电压
D.要想在荧光屏上出现一条正弦曲线,需在偏转电极XX'上加适当频率的扫描电压、在偏转电极YY'上加按正弦规律变化的电压
答案:A
解析:要想让亮斑沿OY向上移动,电子受力方向应沿Y方向,即Y电势高,选项A错误;要想让亮斑移到荧光屏的右上方,Y为高电势,X为高电势才可以,选项B正确;要想在荧光屏上出现一条水平亮线,要在XX'上加扫描电压,在YY'上加恒定电压或不加电压,选项C正确;要想在荧光屏上出现一条正弦曲线,分析可知选项D正确。

如图是示波管的示意图,从电子枪发出的电子通过两对偏转电极,如果偏转电极不加电压,则电子沿直线打在荧光屏的中心O,当在两对偏转电极上同时加上电压后,电子将偏离中心打在某个位置,现已标出偏转电极所加电压的正负极,从示波管的右侧来看,电子可能会打在荧光屏上哪一位置( )
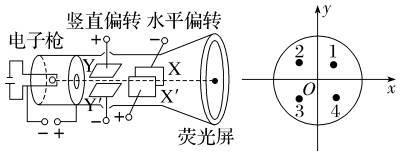
A.1位置 B.2位置 C.3位置 D.4位置
解析:B 根据竖直和水平偏转电压的正、负极,带负电的电子应偏向屏幕的左上方,故选B。

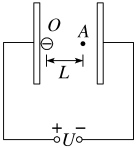
1.两平行金属板相距为d,电势差为U,一电子质量为m,电荷量为e,从O点沿垂直于极板的方向射出,最远到达A点,然后返回,如图所示,OA=L,则此电子具有的初动能是( )
A.![]() B.edUL C.
B.edUL C.![]() D.
D.![]()
解析:D 电子从O点运动到A点,因受静电力作用,速度逐渐减小。根据题意和题图判断,电子仅受静电力,不计重力。根据动能定理得eUOA= m
m![]() 。因E=
。因E= ,UOA=EL=
,UOA=EL=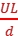 ,所以
,所以 m
m![]() =
=![]() 。故选D。
。故选D。
2.(2023·江苏苏州高二月考)喷墨打印机的简化模型如图所示。重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( )
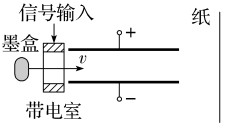
A.向负极板偏转
B.电势能逐渐增大
C.运动轨迹是抛物线的一部分
D.运动轨迹与带电荷量有关
解析:C 由于微滴带负电,其所受电场力指向正极板,故微滴在电场中向正极板偏转,A错误;微滴在电场中所受的电场力对微滴做正功,微滴的电势能减小,B错误;由于极板间电场是匀强电场,电场力不变且与微滴的初速度方向垂直,故微滴在电场中做匀变速曲线运动,并且轨迹为抛物线的一部分,C正确;设微滴带电荷量为q,质量为m,经过t时间在电场中沿电场线方向的位移为y,y= at2=
at2=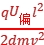 ,又qU加=
,又qU加= mv2,故y=
mv2,故y=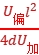 ,则微滴在极板间电场中的运动轨迹与其带电荷量无关,D错误。
,则微滴在极板间电场中的运动轨迹与其带电荷量无关,D错误。
3.如图所示,质子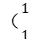 H)和α粒子
H)和α粒子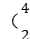 He)以相同的初动能垂直射入偏转电场(粒子不计重力),这两个粒子都能射出电场,α粒子的质量是质子的4倍,带电荷量是质子的2倍,则质子和α粒子射出电场时的侧位移y之比为( )
He)以相同的初动能垂直射入偏转电场(粒子不计重力),这两个粒子都能射出电场,α粒子的质量是质子的4倍,带电荷量是质子的2倍,则质子和α粒子射出电场时的侧位移y之比为( )
A.1∶1 B.1∶2
C.2∶1 D.1∶4
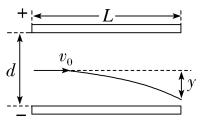
解析:B 根据侧位移计算公式y= ·
·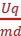 ·
·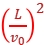 以及动能表达式Ek=
以及动能表达式Ek= m
m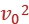 得y=
得y=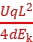 ,初动能相同,α粒子的带电荷量是质子的2倍,解得y1∶y2=1∶2。故B正确。
,初动能相同,α粒子的带电荷量是质子的2倍,解得y1∶y2=1∶2。故B正确。
4.两平行金属板A、B水平放置,一个质量为m=5×10-6 kg的带电微粒,以v0=2 m/s的水平速度从两板正中位置射入电场,如图所示,A、B两板间距离为d=4 cm,板长l=10 cm。(g取10 m/s2)
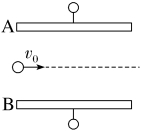
(1)当A、B间的电压为UAB=1 000 V时,微粒恰好不偏转,沿图中虚线射出电场,求该微粒的电荷量和电性;
(2)使B板接地,欲使该微粒射出偏转电场,求A板电势的取值范围。
答案:(1)2×10-9 C 负 (2)-600 V~2 600 V
解析:(1)当重力跟静电力大小相等、方向相反时,微粒才沿初速度v0方向做匀速直线运动,故有q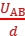 =mg,得q=
=mg,得q=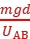 =2×10-9C;重力方向竖直向下,则静电力方向竖直向上,而电场强度方向竖直向下(UAB>0),所以微粒带负电。
=2×10-9C;重力方向竖直向下,则静电力方向竖直向上,而电场强度方向竖直向下(UAB>0),所以微粒带负电。
(2)当静电力方向竖直向上,且qE>mg时,带电微粒向上偏转,设微粒从右上边缘飞出时φA=φ1,因为φB=0,所以UAB'=φ1,静电力和重力都沿竖直方向,微粒在水平方向做匀速直线运动,水平方向上有l=v0t。在竖直方向上有a=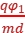 -g,偏转位移y=
-g,偏转位移y= =
= at2,联立解得φ1=
at2,联立解得φ1=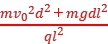 =2 600 V。当静电力方向竖直向下时,带电微粒向下偏转,此时设φA=φ2,则竖直方向上有a'=g-
=2 600 V。当静电力方向竖直向下时,带电微粒向下偏转,此时设φA=φ2,则竖直方向上有a'=g-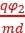 ,同理可得φ2=-600 V,故欲使微粒射出偏转电场,A板电势的取值范围为-600 V~2 600 V。
,同理可得φ2=-600 V,故欲使微粒射出偏转电场,A板电势的取值范围为-600 V~2 600 V。

![]()
考点一 带电粒子在电场中的加速
1.质量和电荷量不同的带电粒子,在电场中由静止开始经相同电压加速后( )
A.比荷大的粒子速度大,电荷量大的粒子动能大
B.比荷大的粒子动能大,电荷量大的粒子速度大
C.比荷大的粒子速度和动能都大
D.电荷量大的粒子速度和动能都大
解析:A 根据动能定理得qU= mv2,解得v=
mv2,解得v=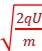 ,根据上式可知,经相同电压加速后,比荷
,根据上式可知,经相同电压加速后,比荷 大的粒子速度v大,电荷量q大的粒子动能大,故A正确,B、C、D错误。
大的粒子速度v大,电荷量q大的粒子动能大,故A正确,B、C、D错误。
2.如图所示,在P板附近有一电子由静止开始向Q板运动。已知两极板间电势差为U,板间距离为d,电子质量为m,电荷量为e。则关于电子在两板间的运动情况,下列叙述正确的是( )
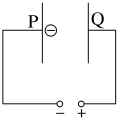
A.若将板间距离d增大一倍,则电子到达Q板时的速率保持不变
B.若将板间距离d增大一倍,则电子到达Q板时的速率也增大一倍
C.若将两极板间电势差U增大一倍,则电子到达Q板的时间保持不变
D.若将两极板间电势差U增大一倍,则电子到达Q板的时间减为原来的一半
解析:A 根据动能定理得eU= mv2,可知电子到达Q板时的速率为v=
mv2,可知电子到达Q板时的速率为v= ,将板间距离增大一倍,因为电压不变,电子到达Q板时的速率不变,A正确,B错误;电子的加速度为a=
,将板间距离增大一倍,因为电压不变,电子到达Q板时的速率不变,A正确,B错误;电子的加速度为a= =
=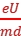 ,根据d=
,根据d= at2得t=d
at2得t=d ,若将两极板间电势差U增大一倍,则电子到达Q板的时间减为原来的
,若将两极板间电势差U增大一倍,则电子到达Q板的时间减为原来的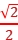 ,C、D错误。
,C、D错误。
3.如图所示,在点电荷+Q激发的电场中有A、B两点,将质子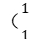 H)和α粒子
H)和α粒子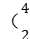 He)分别从A点由静止释放到达B点时,它们的速度大小之比为( )
He)分别从A点由静止释放到达B点时,它们的速度大小之比为( )

A.1∶2 B.2∶1
C.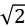 ∶1 D.1∶
∶1 D.1∶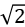
解析:C 质子和α粒子都带正电,从A点释放将受静电力作用加速运动到B点,设A、B两点间的电势差为U,由动能定理可知,对质子: mH
mH![]() =qHU
=qHU
对α粒子: mα
mα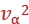 =qαU
=qαU
所以 =
= =
= 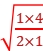 =
=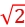 ∶1。
∶1。
4.(2023·江苏溧阳高二期中)当今医学上对某些肿瘤采用质子疗法进行治疗,该疗法用一定能量的质子束照射肿瘤杀死癌细胞,如图所示。现用一直线加速器来加速质子,使其从静止开始被加速到1.0×107 m/s。已知加速电场的场强为1.3×105 N/C,质子的质量为1.67×10-27 kg,电荷量为1.6×10-19 C,则下列说法正确的是( )

A.加速过程中质子电势能增加
B.质子所受到的电场力约为2×10-15 N
C.质子加速需要的时间约为8×10-6 s
D.加速器加速的直线长度约为4 m
解析:D 电场力对质子做正功,质子的电势能减少,A错误;质子受到的电场力大小F=qE≈2×10-14 N,B错误;质子的加速度a= ≈1.2×1013 m/s2,加速时间t=
≈1.2×1013 m/s2,加速时间t= ≈8×10-7 s,C错误;加速器加速的直线长度x=
≈8×10-7 s,C错误;加速器加速的直线长度x= ≈4 m,D正确。
≈4 m,D正确。
考点二 带电粒子在电场中的偏转
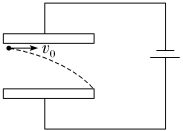
5.如图所示,两极板与电源相连接,电子从负极板边缘垂直电场方向射入匀强电场,且恰好从正极板边缘飞出,现在使电子入射速度变为原来的两倍,而电子仍从原位置射入,且仍从正极板边缘飞出,则两极板的间距应变为原来的( )
A.2倍 B.4倍
C. D.
D.
解析:C 电子在两极板间做类平抛运动,水平方向l=v0t,t= ,竖直方向d=
,竖直方向d= at2=
at2=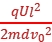 ,故d2=
,故d2=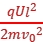 ,即dv0=
,即dv0=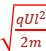 (定值),故C正确。
(定值),故C正确。
6.如图所示,一电子枪发射出的电子(初速度很小,可视为零)进入加速电场加速后,垂直射入偏转电场,射出时偏转位移为y,要使偏转位移增大,下列可行的措施是( )
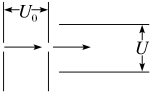
A.增大偏转电压U
B.增大加速电压U0
C.增大偏转极板间距离
D.将发射电子改成发射负离子
解析:A 设电子经加速电场加速后的速度为v,则有 mv2=eU0,所以电子进入偏转电场时速度的大小为v=
mv2=eU0,所以电子进入偏转电场时速度的大小为v=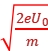 ,电子进入偏转电场后的偏转位移y=
,电子进入偏转电场后的偏转位移y= at2=
at2= ·
·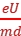 ·
·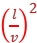 =
=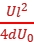 。可见,要增大y,可行的方法有:增大偏转电压U,减小加速电压U0,减小偏转电场极板间距离d。选项A正确。
。可见,要增大y,可行的方法有:增大偏转电压U,减小加速电压U0,减小偏转电场极板间距离d。选项A正确。
7.三个电子在同一地点沿同一直线垂直飞入偏转电场,不计电子重力,如图,a打在下极板上,b正好飞出。则由此可判断( )
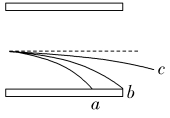
A.b和c同时飞离电场
B.在b飞离电场的瞬间,a刚好打在下极板上
C.进入电场时,a速度最大,c速度最小
D.c的动能增量最大,a和b的动能增量一样大
解析:B 三个电子的质量和电荷量都相同,可知加速度相同,a、b两电子在竖直方向上的位移相等,根据y= at2 可知运动时间相等,故B正确;b、c竖直方向上的位移不等,yc<yb,根据y=
at2 可知运动时间相等,故B正确;b、c竖直方向上的位移不等,yc<yb,根据y= at2,可知tc<tb,故A错误;在垂直于电场方向即水平方向,三个电子做匀速直线运动,则有v=
at2,可知tc<tb,故A错误;在垂直于电场方向即水平方向,三个电子做匀速直线运动,则有v= ,因xc=xb,tc<tb,则vc>vb,根据ta=tb,xb>xa,则vb>va,所以有vc>vb>va,故C错误;根据动能定理知,a、b两电荷静电力做功一样多,所以动能增加量相等,离开电场时c电荷偏移最小,静电力做功最少,动能增加量最少,故D错误。
,因xc=xb,tc<tb,则vc>vb,根据ta=tb,xb>xa,则vb>va,所以有vc>vb>va,故C错误;根据动能定理知,a、b两电荷静电力做功一样多,所以动能增加量相等,离开电场时c电荷偏移最小,静电力做功最少,动能增加量最少,故D错误。
8.示波器能把肉眼看不见的电信号变换成看得见的图像,便于人们研究各种电现象的变化过程。示波器部分结构如图所示,金属丝发射出来的电子(速度可忽略)被加速后从金属板的小孔穿出,从极板正中央垂直射入偏转电场,偏转后射出电场。已知加速电压为U1,两板间电压为U2,板间距为d,板长为L,电子的比荷为 。
。
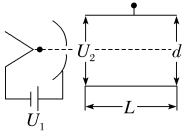
(1)求电子进入偏转电场时的速度v0的大小;
(2)若L=d=8 cm,U2=400 V,U1=200 V,求电子离开偏转电场时偏离原入射方向的侧移距离y的大小。
答案:(1) (2)4 cm
(2)4 cm
解析:(1)由动能定理得eU1= m
m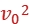 -0
-0
解得v0= 。
。
(2)水平方向上有L=v0t
竖直方向上有y= at2
at2
又eE=ma,E=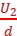
解得y=4 cm。

9.如图所示,三块平行放置的带电金属薄板A、B、C中央各有一小孔,小孔分别位于O、M、P点。由O点静止释放的电子恰好能运动到P点。现将C板向右平移到P'点,则由O点静止释放的电子( )
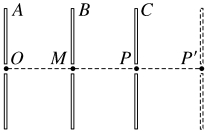
A.运动到P点返回
B.运动到P和P'点之间返回
C.运动到P'点返回
D.穿过P'点
解析:A 设AB、BC间的电场强度分别为E1、E2,间距分别为d1和d2,电子由O点运动到P点的过程中,根据动能定理得:eE1d1-eE2d2=0 ①
当C板向右平移后,BC板间的电场强度
E2'= =
=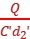 =
=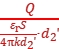 =
=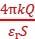
BC板间的电场强度与板间距无关,大小不变。
第二次释放后,设电子在B、C间移动的距离为x,则eE1d1-eE2x=0-0 ②
比较①②两式知,x=d2,即电子运动到P点时返回,选项A正确。
10.如图所示,一个带正电粒子以一定的初速度v0沿两板的中线进入水平放置的平行金属板内,恰好沿下板的边缘飞出,已知板长为L,平行板间距离为d,板间电压为U,带电粒子的质量为m,不计粒子的重力,则( )
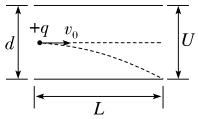
A.粒子的电荷量q=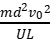
B.粒子动能增加量为![]()
C.在粒子运动前一半时间和后一半时间的过程中,静电力做功之比为1∶3
D.在粒子运动前一半时间和后一半时间的过程中,静电力做功之比为1∶2
解析:C 粒子在竖直方向做初速度为零的匀加速直线运动,则 =
= ·a·t2,粒子的加速度a=
·a·t2,粒子的加速度a= ,粒子运动的时间t=
,粒子运动的时间t= ,联立可得q=
,联立可得q=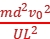 ,A错误;带正电的粒子以一定的初速度v0沿两板的中线进入水平放置的平行金属板内,恰好沿下板的边缘飞出,粒子动能增加量为ΔEk=
,A错误;带正电的粒子以一定的初速度v0沿两板的中线进入水平放置的平行金属板内,恰好沿下板的边缘飞出,粒子动能增加量为ΔEk= qU=
qU=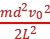 ,B错误;设粒子在前一半时间内和在后一半时间内竖直位移分别为y1、y2,由于粒子竖直方向做初速度为零的匀加速直线运动,则y1∶y2=1∶3,得y1=
,B错误;设粒子在前一半时间内和在后一半时间内竖直位移分别为y1、y2,由于粒子竖直方向做初速度为零的匀加速直线运动,则y1∶y2=1∶3,得y1= d,y2=
d,y2= d,在前一半时间内,静电力对粒子做的功为W1=
d,在前一半时间内,静电力对粒子做的功为W1= qU,在后一半时间内,静电力对粒子做的功为W2=
qU,在后一半时间内,静电力对粒子做的功为W2= qU,静电力做功之比为1∶3,D错误,C正确。
qU,静电力做功之比为1∶3,D错误,C正确。
11.(2023·江苏句容高二校联考)如图所示,带等量异种电荷的两正对平行金属板M、N间存在匀强电场,板长为L(不考虑边界效应)。t=0时刻,M板中点处的粒子源发射两个速度大小为v0的相同粒子,垂直M板向右的粒子,到达N板时速度大小为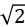 v0;平行M板向下的粒子,刚好从N板下端射出。不计重力和粒子间的相互作用,则( )
v0;平行M板向下的粒子,刚好从N板下端射出。不计重力和粒子间的相互作用,则( )
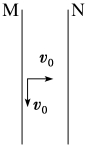
A.M板电势高于N板电势
B.两个粒子的电势能都增加
C.粒子在两板间的加速度为a=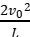
D.粒子从N板下端射出的时间t=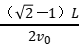
解析:C 粒子的电性未知,粒子从M极板到N极板,电场力做正功,但不能判断极板电势的高低,A错误;电场力做正功时,粒子电势能减小,B错误;根据动能定理可知,平行M板向下的粒子,到达N极板下端时的速度大小仍为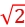 v0,在平行极板方向做匀速运动,速度为v0,在垂直极板方向做匀加速直线运动,有a=
v0,在平行极板方向做匀速运动,速度为v0,在垂直极板方向做匀加速直线运动,有a= ,t=
,t= ,解得a=
,解得a=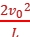 ,C正确,D错误。
,C正确,D错误。
12.如图所示为一真空示波管,电子从位于中心线上的灯丝K发出(初速度不计),经灯丝与A板间的加速电压U1加速,从A板中心孔沿中心线KO射出,然后进入两块带电平行金属板M、N形成的偏转电场中(偏转电场可视为匀强电场),电子进入M、N间电场时的速度与电场方向垂直,电子经过偏转电场后打在荧光屏上的P点。已知M、N两板间的电压为U2,两板间的距离为d,板长为L1,板右端到荧光屏的距离为L2,电子质量为m,电荷量为e,求:
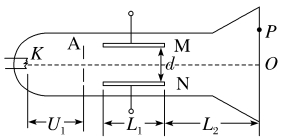
(1)电子穿过A板时的速度大小v0;
(2)电子从偏转电场射出时的侧移量y;
(3)P点到O点的距离Y;
(4)该示波器的灵敏度D(荧光屏上每单位偏转电压引起的偏转量)。
答案:(1) (2)
(2)
(3)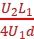 (L1+2L2) (4)
(L1+2L2) (4)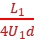 (L1+2L2)
(L1+2L2)
解析:(1)对电子从K发出到穿过A板中心孔,由动能定理得eU1= m
m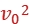
解得v0= 。
。
(2)电子在偏转电场中做类平抛运动
沿偏转电场方向有e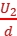 =ma,y=
=ma,y= at2
at2
垂直偏转电场方向有L1=v0t
解得y=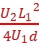 。
。
(3)设电子离开偏转电场时沿电场方向的速度为vy,偏转角为θ,离开偏转电场到打在P点的过程中的侧移量为y',则
vy=at,tan θ= ,y'=tan θ·L2,Y=y+y'
,y'=tan θ·L2,Y=y+y'
解得Y=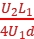 (L1+2L2)。
(L1+2L2)。
(4)该示波器的灵敏度D= =
=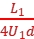 (L1+2L2)。
(L1+2L2)。
1、本网站所提供的信息,只供教育教学参考之用。
2、本网站及其会员一概毋须以任何方式就任何信息传递或传送的失误、不准确或错误对用户或任何其他人士负任何直接或间接的责任。
3、在法律允许的范围内,本网站在此声明,不承担用户或任何人士就使用或未能使用本网站所提供的信息或任何链接或项目所引致的任何直接、间接、附带、从属、特殊、惩罚性或惩戒性的损害赔偿。
4、访问者在从事与本网站相关的所有行为(包括但不限于访问浏览、利用、转载、宣传介绍)时,必须以善意且谨慎的态度行事;访问者不得故意或者过失的损害本网站的各类合法权益,不得利用本网站以任何方式直接或者间接的从事违反中华人民共和国法律、国际公约以及社会公德的行为。对于访问者利用本网站提供的信息而作出的任何决策、决定以及其后果,本网站不承担任何责任
5、本网站图片,文字之类版权,本网站无法鉴别所上传图片或文字的知识版权,如果侵犯,请及时通知我们,本网站将在第一时间及时删除。
6、凡以任何方式登录本网站或直接、间接使用本网站资料者,视为自愿接受本网站声明的约束。
XueXi Design
