

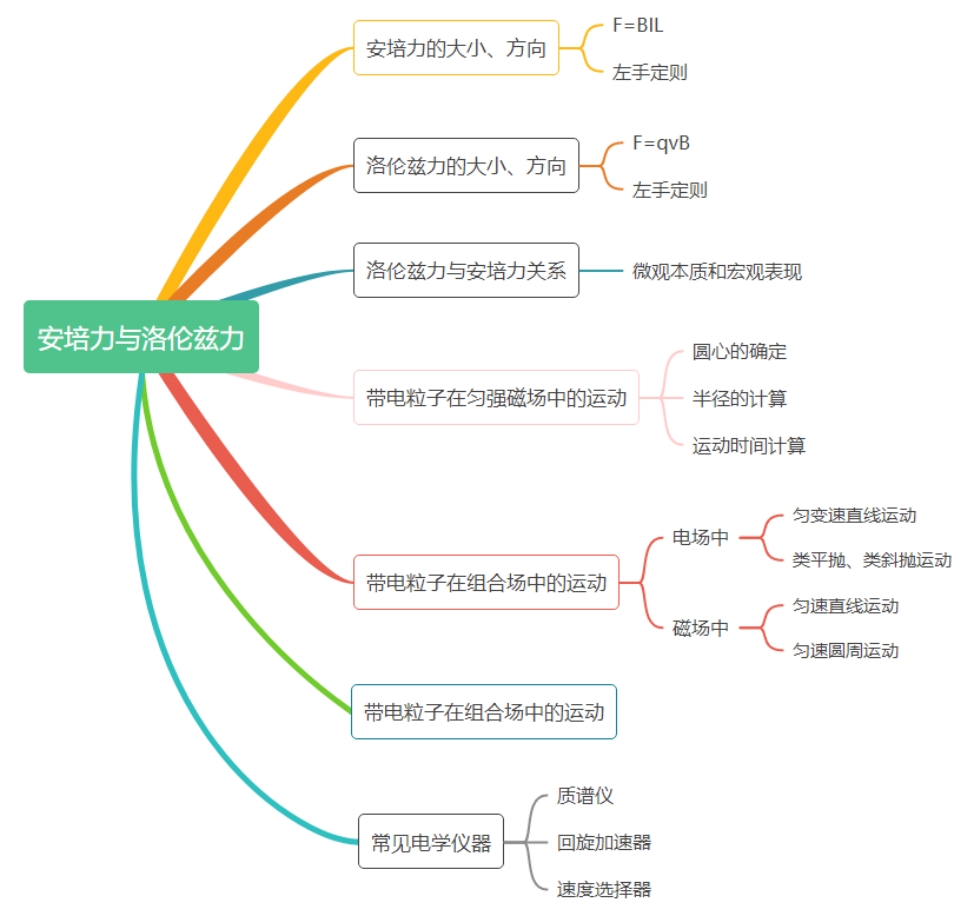

【考点1 安培力的方向】
1.安培力: 通电导体 在磁场中受的力。
2.左手定则:伸开左手,使拇指与其余四个手指垂直,并且都与手掌在同一个平面内;让磁感线 从掌心进入 ,并使四指指向 电流 的方向,这时 拇指所指的方向 就是通电导线在磁场中所受安培力的方向。
3.安培力方向、磁场方向、电流方向的关系。
F⊥B、F⊥I,即F垂直于B和I所决定的平面。
【考点2 安培力的大小】
三种情形(3)B与I成θ角时:F=BILsin θ.
公式适用条件:导线所处的磁场应为 匀强 磁场;在非匀强磁场中,公式仅适用于很短的通电导线。
安培力易错点辨析:
1.对安培力F=BILsin θ的理解
(1)θ是 B 与 I 的夹角,当B与I垂直,即θ=90°时,F=ILB;当B与I成θ角时,F=ILBsin θ。
(2)公式F=BILsin θ中:
①B对放入的通电导线来说是外磁场的磁感应强度,不必考虑导线自身产生的磁感应强度的影响。
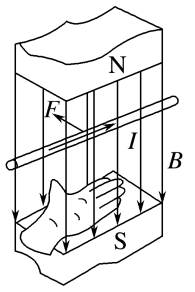
②L是 有效长度 ,匀强磁场中弯曲导线的有效长度L,等于连接两端点直线的长度(如图);相应的电流沿L由始端流向末端。
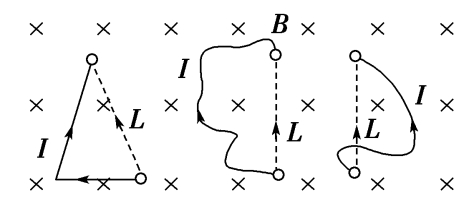
【考点3 洛伦兹力的方向】
1.洛伦兹力
(1)定义: 运动电荷 在磁场中受到的力。
(2)与安培力的关系:通电导线在磁场中受到的安培力是洛伦兹力的宏观表现。
2.洛伦兹力的方向
左手定则:伸开左手,使拇指与其余四个手指 垂直 ,并且都与手掌在同一个平面内,让磁感线从 掌心 垂直进入,并使 四指 指向正电荷运动的方向,或负电荷运动方向的 反向 ,则 拇指 所指的方向就是运动的电荷在磁场中所受洛伦兹力的方向。
【考点4 洛伦兹力的大小】
(1)当v与B成θ角时,F=qvBsinθ
(2)当v⊥B时,F=qvB
(3)当v∥B时,F=0
θ为 电荷运动 方向与 磁感应强度 方向的夹角
洛伦兹力易错点辨析:
1.洛伦兹力的方向总是与电荷运动的方向及磁场方向垂直,即洛伦兹力的方向总是垂直于运动电荷速度方向和磁场方向确定的平面.即F、B、v三个量的方向关系是:F⊥B,F⊥v,但B与v不一定垂直,如图甲、乙所示。
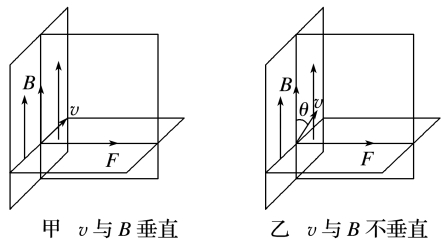
2.在用左手定则判断运动的电荷在磁场中所受洛伦兹力的方向时,对于正电荷,四指指向电荷的运动方向;但对于负电荷,四指应指向电荷运动的反方向。
【考点5 洛伦兹力与安培力的关系】
(1)安培力是导体中所有定向移动的自由电荷受到的洛伦兹力的宏观表现,而洛伦兹力是安培力的微观本质。
(2)洛伦兹力对电荷不做功,但安培力却可以对导体做功。
对应力内容项目 | 洛伦兹力 | 电场力 |
性质 | 磁场对在其中运动的电荷的作用力 | 电场对放入其中电荷的作用力 |
产生条件 | v≠0且v不与B平行 | 电场中无论电荷处于何种状态F≠0 |
大小 | F=qvB(v⊥B) | F=qE |
方向 | 满足左手定则F⊥B、F⊥v | 正电荷受力方向与电场方向相同,负电荷受力方向与电场方向相反 |
做功情况 | 任何情况下都不做功 | 可能做正功、负功,也可能不做功 |
作用效果 | 只改变电荷运动的速度方向,不改变速度大小 | 既可以改变电荷运动的速度大小,也可以改变电荷运动的方向 |
【考点6 带电粒子在匀强磁场中的运动】【重点】
一、带电粒子在匀强磁场中的运动
1.若v∥B,带电粒子以速度v做匀速直线运动,其所受洛伦兹力F= 0
2.若v⊥B,此时初速度方向、洛伦兹力的方向均与磁场方向 垂直 ,粒子在垂直于 磁场 方向的平面内做 匀速圆周 运动。
洛伦兹力提供向心力,只改变粒子速度的 方向 ,不改变粒子速度的 大小 。
二、带电粒子在磁场中做圆周运动的半径和周期
1.由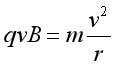 ,可得
,可得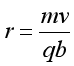
2.由![]() 和
和![]() ,可得
,可得![]() 。
。
带电粒子在匀强磁场中做匀速圆周运动的周期与轨道半径和运动速度 无关 。
三、带电粒子在匀强磁场中的圆周运动
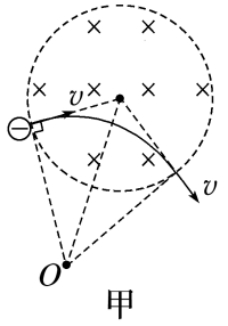
1.圆心的确定
(1)若已知粒子轨迹上的两点的速度方向,分别确定两点处洛伦兹力F的方向,其交点即为圆心,如图甲。
(2)若已知粒子运动轨迹上的两点和其中某一点的速度方向,弦的中垂线与速度垂线的交点即为圆心,如图乙。
(3)若已知粒子轨迹上某点速度方向,又能根据r=qB计算出轨迹半径r,则在该点沿洛伦兹力方向距离为r的位置为圆心,如图丙。
2.半径的计算方法
方法一:由 求得
求得
方法二:连半径构出三角形,由数学方法解三角形或勾股定理求得
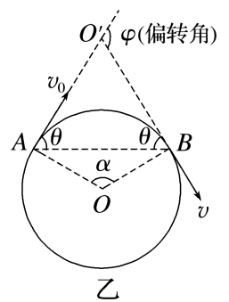
例如:如图甲,R=sin θ或由R2=L2+(R-d)2求得

常用到的几何关系
①粒子的偏转角等于半径扫过的圆心角,如图乙,φ=α
②弦切角等于弦所对应圆心角一半,θ=2α.
3.时间的计算方法
方法一 利用圆心角、周期求得t=2πT
方法二 利用弧长、线速度求得t=v
四、带电粒子在有界磁场中的运动
1.直线边界(进出磁场具有对称性,如图所示)
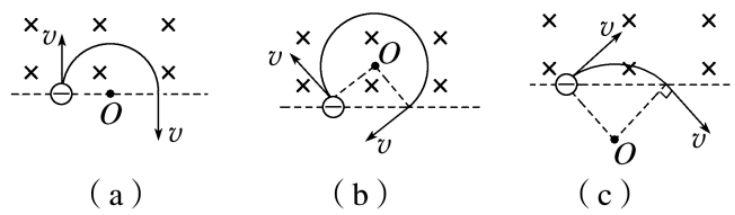
2.平行边界(往往存在临界条件,如图所示)
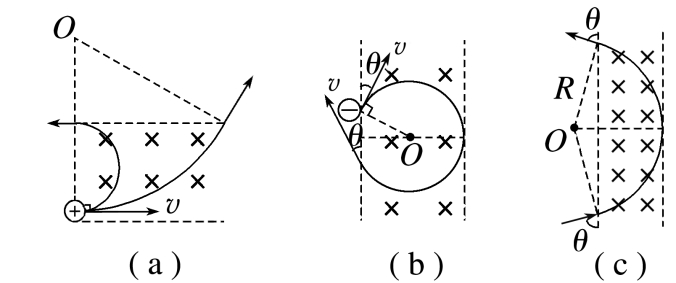
3.圆形边界(进出磁场具有对称性)
(1)沿径向射入必沿径向射出,如图甲所示.
(2)不沿径向射入时,如图乙所示.
射入时粒子速度方向与半径的夹角为θ,射出磁场时速度方向与半径的夹角也为θ.

【考点7:带电粒子在组合场中的运动】(重点、难点)
1.组合场:电场与磁场各位于一定的区域内,并不重叠,或在同一区域,电场、磁场交替出现.
2.分析思路
(1)划分过程:将粒子运动的过程划分为几个不同的阶段,对不同的阶段选取不同的规律处理.
(2)找关键点:确定带电粒子在场区边界的速度(包括大小和方向)是解决该类问题的关键.
(3)画运动轨迹:根据受力分析和运动分析,大致画出粒子的运动轨迹图,有利于形象、直观地解决问题.
3.常见粒子的运动及解题方法
【考点8:带电粒子在叠加场中的运动】(重点、难点)
1.叠加场
电场、磁场、重力场共存,或其中某两场共存。
2.洛伦兹力、重力并存
(1)若重力和洛伦兹力平衡,则带电粒子做匀速直线运动。
(2)若重力和洛伦兹力不平衡,则带电粒子将做复杂的曲线运动,因洛伦兹力不做功,故机械能守恒。
3.电场力、洛伦兹力并存(不计重力的微观粒子)
(1)若电场力和洛伦兹力平衡,则带电粒子做匀速直线运动。
(2)若电场力和洛伦兹力不平衡,则带电粒子将做复杂的曲线运动,因洛伦兹力不做功,可用动能定理求解。
4.电场力、洛伦兹力、重力并存
(1)若三力平衡,带电粒子一定做匀速直线运动。
(2)若重力与电场力平衡,一定做匀速圆周运动。
(3)若合力不为零且与速度方向不垂直,将做复杂的曲线运动,因洛伦兹力不做功,可用能量守恒定律或动能定理求解。
【考点9 常见电学仪器】
一、质谱仪
1.质谱仪构造:主要构件有加速 电场 、偏转 磁场 和照相底片。
2.运动过程(如图)
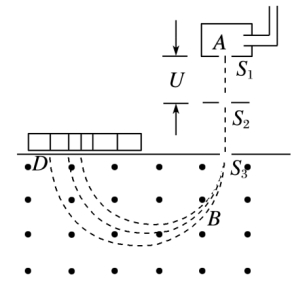
(1)带电粒子经过电压为U的加速电场加速,qU=2mv2
(2)垂直进入磁感应强度为B的匀强磁场中,做匀速圆周运动,r=qB,可得r=Bq
3.分析:从粒子打在底片D上的位置可以测出圆周的半径r,进而可以算出粒子的 比荷
二、回旋加速器
1.回旋加速器的构造:两个D形盒,两D形盒接交流电源,D形盒处于垂直于D形盒的匀强磁场中,如图
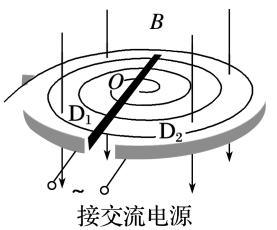
2.工作原理
(1)电场的特点及作用
特点:两个D形盒之间的窄缝区域存在 周期性变化 的电场
作用:带电粒子经过该区域时被 加速
(2)磁场的特点及作用
特点:D形盒处于与盒面垂直的 匀强 磁场中
作用:带电粒子在洛伦兹力作用下做 匀速圆周 运动,从而改变运动 方向 ,半个圆周后再次进入电场
技巧归纳
回旋加速器两D形盒之间有窄缝,中心附近放置粒子源(如质子、氘核或α粒子源),D形盒间接上交流电源,在狭缝中形成一个交变电场。D形盒上有垂直盒面的匀强磁场(如图所示)
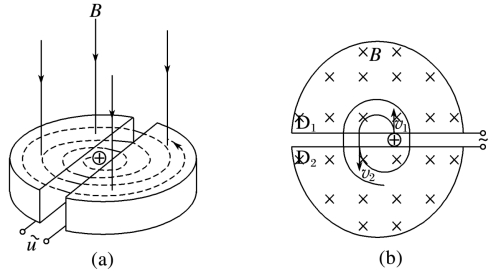
(1)电场的特点及作用
特点:周期性变化,其周期等于粒子在磁场中做圆周运动的周期.
作用:对带电粒子加速,粒子的动能增大,qU=ΔEk.
(2)磁场的作用:改变粒子的运动方向
粒子在一个D形盒中运动半个周期,运动至狭缝进入电场被加速.磁场中qvB=mr,r=qB∝v,因此加速后的轨迹半径要大于加速前的轨迹半径
(3)粒子获得的最大动能
若D形盒的最大半径为R,磁感应强度为B,由r=qB得粒子获得的最大速度vm=m,最大动能Ekm=2mvm2=2m
(4)两D形盒窄缝所加的交流电源的周期与粒子做圆周运动的周期相同,粒子经过窄缝处均被加速,一个周期内加速两次
三 、速度选择器
①平行板中电场强度E和磁感应强度B互相垂直(如图所示)
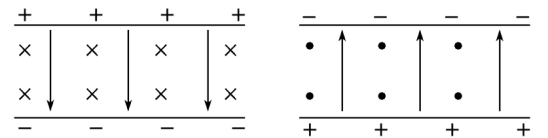
②带电粒子能够沿直线匀速通过速度选择器的条件是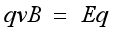 ,即
,即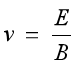
③速度选择器只能选择粒子的速度,不能选择粒子的电性、电荷量、质量
④速度选择器具有单向性
1、本网站所提供的信息,只供教育教学参考之用。
2、本网站及其会员一概毋须以任何方式就任何信息传递或传送的失误、不准确或错误对用户或任何其他人士负任何直接或间接的责任。
3、在法律允许的范围内,本网站在此声明,不承担用户或任何人士就使用或未能使用本网站所提供的信息或任何链接或项目所引致的任何直接、间接、附带、从属、特殊、惩罚性或惩戒性的损害赔偿。
4、访问者在从事与本网站相关的所有行为(包括但不限于访问浏览、利用、转载、宣传介绍)时,必须以善意且谨慎的态度行事;访问者不得故意或者过失的损害本网站的各类合法权益,不得利用本网站以任何方式直接或者间接的从事违反中华人民共和国法律、国际公约以及社会公德的行为。对于访问者利用本网站提供的信息而作出的任何决策、决定以及其后果,本网站不承担任何责任
5、本网站图片,文字之类版权,本网站无法鉴别所上传图片或文字的知识版权,如果侵犯,请及时通知我们,本网站将在第一时间及时删除。
6、凡以任何方式登录本网站或直接、间接使用本网站资料者,视为自愿接受本网站声明的约束。
XueXi Design
