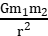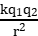2.库仑定律
课标要求 | 素养目标 |
1.了解库仑定律的内涵,具有与库仑力相关的相互作用观念。 2.能在熟悉情境中运用点电荷模型分析问题。 3.体会探究库仑定律过程中的科学思想和方法。 4.了解库仑扭秤实验并能提出相关问题,体会科学研究的一些共性,并进行创新 | 1.通过与质点模型类比,体会将带电体看作点电荷的条件,进一步理解科学研究中的理想模型法。(物理观念) 2.通过探究库仑定律的过程,体会科学思想和方法。(科学探究) 3.通过例题和习题,掌握运用库仑定律分析求解问题的方法。(科学思维) |

知识点一 电荷之间的作用力
1.库仑定律
(1)内容:真空中两个静止点电荷之间的相互作用力,与它们的电荷量的 乘积 成正比,与它们的距离的 二次方 成反比,作用力的方向在它们的连线上。
(2)适用条件:① 真空 ;② 点电荷 。
2.静电力:电荷之间的相互作用力,也叫库仑力。
3.点电荷: 形状 、大小及电荷分布状况对它们之间的作用力的影响可以 忽略 的带电体,是一种理想化模型。
知识点二 库仑的实验
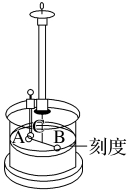
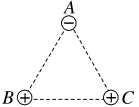
1.实验装置:库仑扭秤(如图所示)
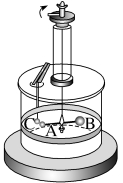
2.实验步骤
(1)改变A和C之间的距离r,记录每次悬丝扭转的角度,便可找出力F与距离r的关系。
(2)根据完全相同的金属小球接触后所带的电荷量相等,改变A和C的带电荷量,记录每次悬丝扭转的角度,便可找出力F与带电荷量q之间的关系。
3.实验结论
(1)力F与距离r的二次方成反比,即F∝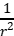 。
。
(2)力F与电荷量q1和q2的乘积成正比,即F∝q1q2。
4.库仑定律表达式:F= k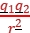 ,其中k叫作静电力常量,k= 9.0×109 N·m2/C2。
,其中k叫作静电力常量,k= 9.0×109 N·m2/C2。
知识点三 静电力计算
1.微观粒子间的万有引力 远小于 库仑力。在研究微观带电粒子的相互作用时,可以把万有引力忽略。
2.如果存在两个以上的电荷,那么,每个点电荷都要受到其他所有电荷对它的作用力。两个或两个以上点电荷对某一个点电荷的作用力,等于各点电荷单独对这个点电荷的作用力的 矢量和 。
【情景思辨】
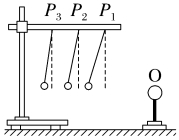
用控制变量法可以研究影响电荷间相互作用力的因素。如图所示,O是一个带电的物体,若把系在绝缘丝线上的带电小球先后挂在横杆上的P1、P2、P3等位置,就可以比较小球在不同位置所受带电物体的作用力的大小,这个力的大小可以通过丝线偏离竖直方向的角度θ显示出来。
(1)探究电荷之间的作用力与某一因素的关系时,必须采用控制变量法。( √ )
(2)只有电荷量很小的带电体才能看成点电荷。( × )
(3)两点电荷所带的电荷量越大,它们间的静电力就越大。( × )
(4)两点电荷所带的电荷量一定时,电荷间的距离越小,它们间的静电力就越大。( √ )
(5)若点电荷q1的电荷量大于q2的电荷量,则q1对q2的静电力大于q2对q1的静电力。( × )

要点一 库仑定律的理解与应用

【探究】原子结构模型示意图如图所示。该模型中,电子绕原子核做匀速圆周运动,就像地球的卫星一样。

观察图片,思考:电子做匀速圆周运动所需的向心力是由原子核对电子的万有引力提供的吗?
提示:不是,原子核对电子的库仑力提供了向心力,两者间的万有引力要比库仑力小得多,完全可以忽略不计。
【归纳】
1.静电力的大小计算和方向判断
(1)大小计算
利用库仑定律计算静电力的大小时,不必将表示电性的正、负号代入公式,只代入q1、q2的绝对值即可。
(2)方向判断
在两电荷的连线上,同种电荷相斥,异种电荷相吸。
2.库仑定律与万有引力定律的比较
比较项目 | 万有引力定律 | 库仑定律 |
公式 | F= | F= |
力的效果 | 只能是引力 | 既可以是引力,也可以是斥力 |
适用条件 | 质点或质量分布均匀的球体 | 真空中静止的点电荷 |
常数 | 引力常量G | 静电力常量k |
相同点 | 与距离的平方成反比 | |
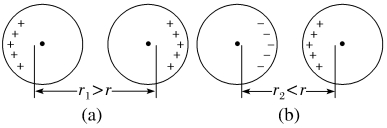
3.两个带电球体间的库仑力
(1)两个规则的均匀带电球体,相距比较远时,可以看成点电荷,也适用库仑定律,球心间的距离就是二者的距离。
(2)两个规则的带电球形导体相距比较近时,不能被看作点电荷,此时两带电球体之间的作用距离会随所带电荷量的改变而改变,即电荷的分布会发生改变。若带同种电荷时,如图(a),由于排斥而距离变大,此时F<k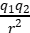 ;若带异种电荷时,如图(b),由于吸引而距离变小,此时F>k
;若带异种电荷时,如图(b),由于吸引而距离变小,此时F>k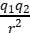 。
。
【典例1】 两个大小相同、可看成点电荷的金属小球a和b,带有等量异种电荷,被固定在绝缘水平面上,这时两球间静电力的大小为F。现用一个不带电且与金属小球a、b大小相同的金属小球c先与a球接触,再与b球接触后移走,则a、b两球间的静电力大小变为( )
A. B.
B.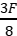
C.![]() D.
D.![]()
答案:D
解析:设a球与b球的电荷量大小均为q,假设a球带正电,则b球带负电,当不带电的小球c与a球接触后,a、c两球平分电荷,每球带电荷量为+ ,当再把c球与b球接触后,两球的电荷先中和再平分,每球所带电荷量为-
,当再把c球与b球接触后,两球的电荷先中和再平分,每球所带电荷量为- ,由库仑定律F=k
,由库仑定律F=k 可知,当移开c球后,由于a、b两球间距离不变,所以a、b两球之间的静电力的大小为F1=
可知,当移开c球后,由于a、b两球间距离不变,所以a、b两球之间的静电力的大小为F1= 。
。
规律方法
解决此类问题的思路
(1)先根据库仑定律写出原来a、b间静电力的表达式;
(2)再根据“两个完全相同的导体球相互接触后电荷量平分”确定接触后a、b各自所带的电荷量;
(3)最后根据库仑定律写出变化后a、b间静电力的表达式。

1.(2023·江苏南京高二校联考)图示的仪器叫库仑扭秤,法国科学家库仑用此装置找到了电荷间相互作用的规律,装置中A、C为带电金属球,两球间静电力大小为F,B为不带电的平衡小球,现将C球电荷量减半,扭转悬丝使A回到初始位置,则A、C两球间静电力大小为( )
A.![]() B.
B.![]()
C.F D.2F
解析:B 根据库仑定律可得F=k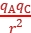 ,将C球电荷量减半,扭转悬丝使A回到初始位置,则A、C两球间距离不变,则A、C两球间静电力大小为
,将C球电荷量减半,扭转悬丝使A回到初始位置,则A、C两球间距离不变,则A、C两球间静电力大小为 ,所以B正确。
,所以B正确。
2.两个分别带有电荷量-Q和+3Q的相同金属小球(均可视为点电荷),固定在相距为r的两处,它们间库仑力的大小为F。两小球相互接触后将其固定距离变为 ,则两球间库仑力的大小为( )
,则两球间库仑力的大小为( )
A.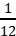 F B.
F B.![]() F
F
C.![]() F D.12F
F D.12F
解析:C 由库仑定律知F=k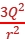 ,当两小球接触后,带电荷量都为Q,故接触后库仑力F'=
,当两小球接触后,带电荷量都为Q,故接触后库仑力F'=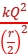 =k
=k![]() ,由以上两式解得F'=
,由以上两式解得F'= F,故C正确。
F,故C正确。
要点二 静电力的叠加

1.两个或三个以上点电荷对某一点电荷的作用力,等于各点电荷单独对这个点电荷的作用力的矢量和。这个结论叫作静电力叠加原理。
2.静电力具有力的一切性质,静电力叠加原理实际就是力叠加原理的一种具体表现。
3.库仑力是矢量,若电荷受到的两个库仑力不在同一直线上,合成遵循平行四边形定则,如图所示。
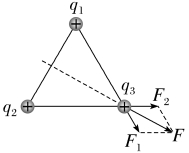
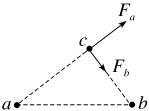
【典例2】 如图所示,三个固定的带电小球a、b和c,相互间的距离分别为ab=5 cm,bc=3 cm,ca=4 cm。小球c所受库仑力的合力的方向平行于a、b的连线。设小球a、b所带电荷量的比值的绝对值为k,则( )
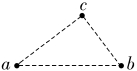
A.a、b带同种电荷,k=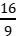
B.a、b带异种电荷,k=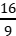
C.a、b带同种电荷,k=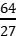
D.a、b带异种电荷,k=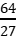
答案:D
解析:如果a、b带同种电荷,则a、b两小球对c的作用力均为斥力或均为引力,此时c在垂直于a、b连线的方向上的合力一定不为零,因此a、b不可能带同种电荷,A、C错误;若a、b带异种电荷,假设a对c的作用力为斥力,则b对c的作用力一定为引力,受力分析如图所示,由题意知c所受库仑力的合力方向平行于a、b的连线,则Fa、Fb在垂直于a、b连线的方向上的合力为零,由相似三角形可知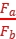 =
= =
= ,结合库仑定律可得
,结合库仑定律可得 =
=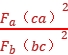 =
= ,同理易知若a对c的作用力为引力,b对c的作用力为斥力,结果相同,B错误,D正确。
,同理易知若a对c的作用力为引力,b对c的作用力为斥力,结果相同,B错误,D正确。
![]()
1.如图所示,有三个点电荷A、B、C位于一个等边三角形的三个顶点上,已知A、B都带正电荷,A所受B、C两个电荷的静电力的合力如图中FA所示,那么可以判定点电荷C所带电荷的电性为( )
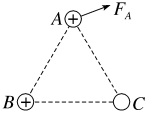
A.一定是正电
B.一定是负电
C.可能是正电,也可能是负电
D.无法判断
解析:B 对点电荷A受力分析,B对A的是库仑斥力,沿BA的连线向上,若C带正电,则C对A的库仑斥力沿CA的连线向上,这两个斥力的合力方向在BA延长线和CA延长线夹角范围内,不包括两条延长线,不可能偏BA延长线向右;若C带负电,C对A的库仑引力沿AC的连线向下,与B对A的库仑斥力的合力偏向BA延长线右侧,所以C一定带负电,故B正确,A、C、D错误。
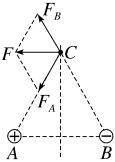
2.如图所示,分别在A、B两点放置电荷量为Q1=+2×10-14 C和Q2=-2×10-14 C的两点电荷。在AB的垂直平分线上有一点C,且AB=AC=BC=6×10-2 m。如果有一电子静止放在C点处,则它所受的库仑力的大小和方向如何?
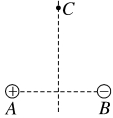
答案:8.0×10-21 N 方向平行于AB连线水平向左
解析:电子带负电荷,在C点同时受A、B两处点电荷的作用力FA、FB,如图所示。由库仑定律F=k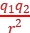 得,FA=k
得,FA=k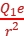 =9.0×109×
=9.0×109×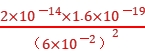 N=8.0×10-21 N,FB=k
N=8.0×10-21 N,FB=k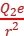 =8.0×10-21 N。由矢量的平行四边形定则和几何知识得静止放在C点的电子受到的库仑力F=FA=FB=8.0×10-21 N,方向平行于AB连线水平向左。
=8.0×10-21 N。由矢量的平行四边形定则和几何知识得静止放在C点的电子受到的库仑力F=FA=FB=8.0×10-21 N,方向平行于AB连线水平向左。
![]()
1.下列对点电荷的认识,正确的是( )
A.只有体积很小的带电体才能看成点电荷
B.体积很大的带电体一定不能看成点电荷
C.只有球形带电体才能看成点电荷
D.当两个带电体的大小远小于它们之间的距离时,可将这两个带电体看成点电荷
解析:D 由带电体看作点电荷的条件可知,当带电体的形状、大小及电荷分布对它们间相互作用力的影响可忽略时,这个带电体可看作点电荷,带电体能否看作点电荷由研究问题的性质决定,与带电体自身大小、形状无关,选项A、B、C错误;当两个带电体的大小远小于它们之间的距离时,两带电体的大小、形状及电荷分布对两带电体间相互作用力的影响可忽略不计,因此可将这两个带电体看成点电荷,选项D正确。
2.两个分别带有电荷量-Q和+7Q的相同金属小球(均可视为点电荷),固定在间距为r的两处,它们之间库仑力的大小为F,两小球相互接触后再分别放回原处,则两球间库仑力的大小为( )
A.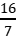 F B.
F B.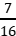 F
F
C.![]() F D.
F D.![]() F
F
解析:D 接触前两个带电小球之间的库仑力大小为F=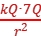 =
=![]() ,接触之后两球所带电荷先中和后均分,故两球所带电荷量均变为+3Q,此时两球之间的库仑力大小为F'=
,接触之后两球所带电荷先中和后均分,故两球所带电荷量均变为+3Q,此时两球之间的库仑力大小为F'=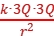 =
=![]() ,解得F'=
,解得F'= F,故D正确。
F,故D正确。
3.如图所示,有三个点电荷A、B、C位于一个等边三角形的三个顶点上,已知三角形的边长为1 cm,B、C所带电荷量为qB=qC=+1×10-6 C,A所带电荷量为qA=-2×10-6 C,静电力常量k=9.0×109 N·m2/C2,A所受B、C两个电荷的静电力的合力F的大小和方向为( )
A.180 N,沿AB方向
B.180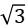 N,沿AC方向
N,沿AC方向
C.180 N,沿∠BAC的角平分线
D.180 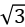 N,沿∠BAC的角平分线
N,沿∠BAC的角平分线
解析:D 点电荷B、C对点电荷A的静电力大小相等,为FBA=FCA=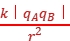 =
=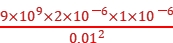 N=180 N,如图所示,A受大小相等的两个静电力,两静电力夹角为60°,由平行四边形定则和几何知识得A受到的静电力的合力大小为F=2FBAcos 30°=2×180×
N=180 N,如图所示,A受大小相等的两个静电力,两静电力夹角为60°,由平行四边形定则和几何知识得A受到的静电力的合力大小为F=2FBAcos 30°=2×180× N=180
N=180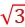 N,方向沿∠BAC的角平分线,故D正确。
N,方向沿∠BAC的角平分线,故D正确。
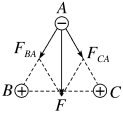
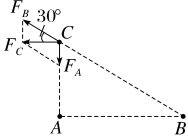
4.(2023·江苏南通高二期中)如图所示,直角三角形ABC中∠B=30°,A、B处的点电荷所带电荷量分别为QA、QB,测得在C处的某正点电荷所受静电力方向平行于AB向左,则下列说法正确的是( )
A.A处的点电荷带正电,QA∶QB=1∶8
B.A处的点电荷带负电,QA∶QB=1∶8
C.A处的点电荷带正电,QA∶QB=1∶4
D.A处的点电荷带负电,QA∶QB=1∶4
解析:B 要使C处的正点电荷所受静电力方向平行于AB向左,该正点电荷所受力的情况应如图所示,所以A带负电,B带正电。设A、C间的距离为L,则B、C间的距离为2L。FBsin 30°=FA,即k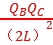 ·sin 30°=
·sin 30°=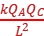 ,解得
,解得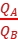 =
= ,故选项B正确。
,故选项B正确。
![]()
![]()
考点一 库仑定律的理解与应用
1.关于点电荷、元电荷,下列说法正确的是( )
A.电子一定可以看成点电荷
B.点电荷所带电荷量一定是元电荷的整数倍
C.形状不规则的带电体不能看成点电荷
D.点电荷、元电荷是同一种物理模型
解析:B 带电体可以看成点电荷的条件是带电体的形状、大小及电荷分布状况对它和其他带电体间相互作用力的影响可忽略不计,与带电体自身大小、形状及所带电荷量无必然联系,选项A、C错误;元电荷是带电体所带电荷量的最小值,因此点电荷所带电荷量一定是元电荷的整数倍,选项B正确;点电荷是物理模型,元电荷是电荷量的最小值,不是物理模型,选项D错误。
2.下列说法正确的是( )
A.美国物理学家密立根发现了电荷之间的相互作用规律
B.若点电荷q1的电荷量大于点电荷q2的电荷量,则q1对q2的静电力大于q2对q1的静电力
C.凡计算真空中两个静止点电荷间的相互作用,都可以使用公式F=k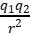
D.根据F=k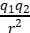 可知,当r→0时,F→∞
可知,当r→0时,F→∞
解析:C 法国物理学家库仑发现了电荷之间的相互作用规律,故A错误;两点电荷之间的作用力是相互的,根据牛顿第三定律可知,无论点电荷q1的电荷量与点电荷q2的电荷量大小关系如何,q1对q2的静电力大小总等于q2对q1的静电力大小,故B错误;库仑定律的适用条件是真空和静止点电荷,如果在研究的问题中,带电体的形状、大小以及电荷分布可以忽略不计,即可将它看成一个几何点,则这样的带电体就是点电荷,一个实际的带电体能否看成点电荷,不仅和带电体本身有关,还取决于问题的性质和精度的要求,故C正确;当r→0时,带电体不能看成点电荷,公式F=k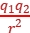 不再适用,故D错误。
不再适用,故D错误。
3.如图所示,两根完全相同的绝缘细线,把两个质量相等的小球悬挂在同一点O上,甲球的电荷量大于乙球的电荷量,则( )
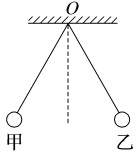
A.甲、乙两球都一定带正电
B.甲、乙两球都一定带负电
C.甲球受到的静电力大于乙球受到的静电力
D.甲、乙两球受到的静电力大小相等
解析:D 依据题图可知,两球之间相互排斥,因此它们带同种电荷,可以是都带正电,也可以是都带负电,究竟带何种电荷不能确定,故A、B错误;两球之间的库仑力属于作用力和反作用力,大小相等,方向相反,故C错误,D正确。
4.真空中有两个静止的点电荷,它们的带电荷量分别为q1、q2,相距R,它们间相互作用的静电力的大小为F。若它们的带电荷量分别变为2q1、4q2,而距离增大为原来的2倍,则它们间的静电力的大小将变为( )
A. B.
B.
C.2F D.8F
解析:C 根据库仑定律知,真空中两个静止点电荷间的静电力大小为F=k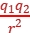 ,若它们的带电荷量分别变为2q1、4q2,而距离增大为原来的2倍,则两点电荷间的静电力大小为F'=k
,若它们的带电荷量分别变为2q1、4q2,而距离增大为原来的2倍,则两点电荷间的静电力大小为F'=k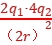 =k
=k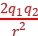 =2F,选项C正确。
=2F,选项C正确。
考点二 静电力的叠加
5.如图所示,在一条直线上的三点分别放置电荷量QA=+3×10-9 C、QB=-4×10-9 C、QC=+3×10-9 C的A、B、C点电荷,则作用在点电荷A上的库仑力的大小为( )
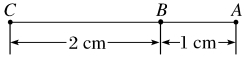
A.9.9×10-4 N B.9.9×10-3 N
C.1.17×10-4 N D.2.7×10-4 N
解析:A A受到B、C点电荷的库仑力,如图所示。根据库仑定律有
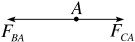
FBA=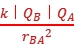 =
=![]() N=1.08×10-3 N,
N=1.08×10-3 N,
FCA=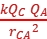 =
=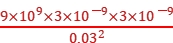 N=9×10-5 N
N=9×10-5 N
规定沿这条直线由A指向C为正方向,则点电荷A受到的合力大小为FA=FBA-FCA=(1.08×10-3-9×10-5)N=9.9×10-4 N,故A正确。
6.如图所示,光滑绝缘的水平地面上有相距为L的点电荷A、B,带电荷量分别为-4Q和+Q,今引入第三个点电荷C,使三个电荷都处于平衡状态,则C的电荷量和放置的位置是( )

A.-Q,在A左侧距A为L处
B.-2Q,在A左侧距A为 处
处
C.-4Q,在B右侧距B为L处
D.+2Q,在A右侧距A为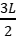 处
处
解析:C 根据电荷受力平衡规律可知,C应放在B的右侧,且与A电性相同,带负电,由FAB=FCB得k =k
=k![]() ,由FAC=FBC得k
,由FAC=FBC得k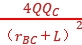 =k
=k![]() ,解得rBC=L,QC=4Q,故选C。
,解得rBC=L,QC=4Q,故选C。
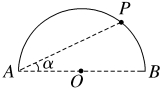
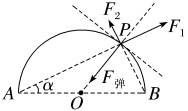
7.(2023·江苏扬州高二期末)如图所示,电荷量分别为Q1、Q2的两个正点电荷分别置于A点和B点,两点相距L,在以AB为直径的光滑绝缘半圆环上,穿着一个带电荷量为q的小球(视为点电荷),小球在P点受力平衡,若不计小球的重力,那么PA与AB的夹角α与Q1、Q2的关系满足( )
A.tan2α=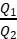 B.tan2α=
B.tan2α=
C.tan3α=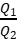 D.tan3α=
D.tan3α=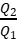
解析:D 对小球进行受力分析,如图所示,设A、B两点与P点的距离分别为r1、r2,根据库仑定律有F1=k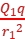 ,F2=k
,F2=k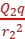 ,由几何关系知r1=Lcos α,r2=Lsin α,根据平衡条件,过P点沿圆环切向方向有F1sin α=F2cos α,解得tan3α=
,由几何关系知r1=Lcos α,r2=Lsin α,根据平衡条件,过P点沿圆环切向方向有F1sin α=F2cos α,解得tan3α= ,故A、B、C错误,D正确。
,故A、B、C错误,D正确。
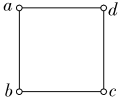
8.如图所示,在边长为l的正方形的每个顶点都放置一个点电荷,其中a和b的电荷量均为+q,c和d电荷量均为-q。静电力常量为k,求a电荷受到的其他三个电荷的静电力的合力。
答案: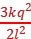
解析:a和b电荷量为+q,c和d电荷量为-q,则c、d电荷对a电荷的静电力为引力,b电荷对a电荷的静电力为斥力。
根据库仑定律可得Fca=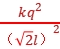 ,Fba=Fda=
,Fba=Fda=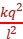 。
。
b、d电荷对a电荷的合力为F合=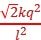 ,其方向与c电荷对a电荷的静电力的夹角为90°。
,其方向与c电荷对a电荷的静电力的夹角为90°。
根据力的合成法则,a电荷受到的其他三个电荷的静电力的合力大小F= =
=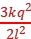 。
。
![]()
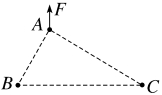
9.如图所示,三个绝缘带电小球A、B、C处于竖直平面内,三个小球的连线构成直角三角形,∠A=90°,∠B=60°。用竖直向上的力F作用在小球A上,三个小球恰好处于静止状态。下列关于三个小球所带电荷量的关系中正确的是( )
A.qA=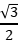 qC B.qA=
qC B.qA= qB
qB
C.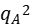 =qBqC D.qB=
=qBqC D.qB=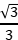 qC
qC
解析:D 由平衡条件可知,A、B间和A、C间必是引力,B、C间必是斥力,故B、C带同种电荷,电性与A相反,对B球受力分析,如图所示
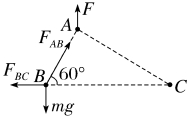
由平衡条件可得FABcos 60°=FBC
同理对于C球满足FACcos 30°=FBC
设A、B距离为l,则A、C距离为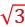 l,B、C距离为2l,由库仑定律可得FAB=k
l,B、C距离为2l,由库仑定律可得FAB=k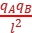 ,FAC=k
,FAC=k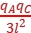 ,FBC=k
,FBC=k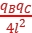 ,联立可得qA∶qB∶qC=
,联立可得qA∶qB∶qC=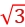 ∶2∶2
∶2∶2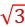 ,D正确。
,D正确。
10.如图所示,一个均匀的带电圆环,带电荷量为+Q,半径为R,放在绝缘水平桌面上。圆心为O点,过O点作一竖直线,在此线上取一点A,使A到O点的距离为R,在A点放一检验电荷+q,则+q在A点所受的库仑力为( )
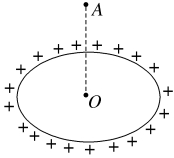
A.![]() ,方向向上 B.
,方向向上 B.![]() ,方向向上
,方向向上
C.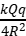 ,方向向上 D.
,方向向上 D.![]() ,方向向上
,方向向上
解析:B 先把带电圆环均分成若干个小部分,每一小部分均可视为点电荷,各点电荷对检验电荷的库仑力在水平方向上相互抵消,竖直向上方向上的库仑力大小为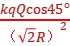 =
=![]() ,故选B。
,故选B。
11.如图所示,半径为R的绝缘球壳上均匀地带有电荷量为+Q的电荷,另一电荷量为+q的点电荷放在球心处,由于对称性,点电荷受力为零。现在球壳上挖去半径为r(r≪R)的一个小圆孔,则此时置于球心的点电荷所受静电力的大小为多少?方向如何?(已知静电力常量为k)
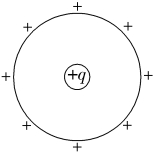
答案: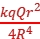 方向由球心指向小圆孔中心
方向由球心指向小圆孔中心
解析:解法1:由于球壳上均匀带电,原来每条直径两端相等的一小块面积上的电荷对球心处点电荷+q的静电力相互平衡。当在球壳上挖去半径为r的小圆孔后,因为是绝缘球壳,其余部分的电荷分布不改变,所以其他直径两端的电荷对球心处点电荷+q的作用力仍相互平衡,剩下的就是与小圆孔相对的半径也为r的一小块圆面上的电荷对它的作用力。又r≪R,所以这一带电小圆面可看成点电荷,库仑定律适用。
小块圆面上的电荷量为q'=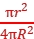 Q=
Q=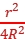 Q
Q
根据库仑定律得它对球心处的点电荷+q的静电力大小F=k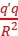 =k
=k![]() =
=![]()
其方向由球心指向小圆孔中心。
解法2:根据中和的特点可知,挖去的小圆孔相当于在此处加上了等量的异种电荷,因为完整球壳对球心处的点电荷的静电力为零,则被挖去小圆孔后的球壳对球心处点电荷的静电力等于在小圆孔处补上的等量异种电荷对该点电荷的作用力。
由库仑定律有F=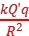
其中Q'=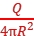 πr2=
πr2=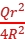 。
。
得出F=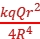 ,方向由球心指向小圆孔中心。
,方向由球心指向小圆孔中心。
12.如图甲、乙所示,两个带电荷量均为q的点电荷分别位于带电荷量线密度相同、半径相同的半圆环和 圆环的圆心,环的粗细可忽略不计。若图甲中环对圆心点电荷的库仑力大小为F,则图乙中环对圆心点电荷的库仑力大小是多少?
圆环的圆心,环的粗细可忽略不计。若图甲中环对圆心点电荷的库仑力大小为F,则图乙中环对圆心点电荷的库仑力大小是多少?
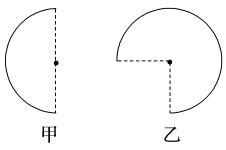
答案: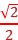 F
F
解析:由题图甲中均匀带电半圆环对圆心点电荷的库仑力大小为F,可以得出 圆环对圆心点电荷的库仑力大小为
圆环对圆心点电荷的库仑力大小为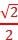 F。将题图乙中的均匀带电
F。将题图乙中的均匀带电 圆环分成三个
圆环分成三个 圆环,关于圆心对称的两个
圆环,关于圆心对称的两个 圆环对圆心点电荷的库仑力的合力为零,因此题图乙中的
圆环对圆心点电荷的库仑力的合力为零,因此题图乙中的 圆环对圆心点电荷的库仑力大小为
圆环对圆心点电荷的库仑力大小为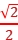 F。
F。
1、本网站所提供的信息,只供教育教学参考之用。
2、本网站及其会员一概毋须以任何方式就任何信息传递或传送的失误、不准确或错误对用户或任何其他人士负任何直接或间接的责任。
3、在法律允许的范围内,本网站在此声明,不承担用户或任何人士就使用或未能使用本网站所提供的信息或任何链接或项目所引致的任何直接、间接、附带、从属、特殊、惩罚性或惩戒性的损害赔偿。
4、访问者在从事与本网站相关的所有行为(包括但不限于访问浏览、利用、转载、宣传介绍)时,必须以善意且谨慎的态度行事;访问者不得故意或者过失的损害本网站的各类合法权益,不得利用本网站以任何方式直接或者间接的从事违反中华人民共和国法律、国际公约以及社会公德的行为。对于访问者利用本网站提供的信息而作出的任何决策、决定以及其后果,本网站不承担任何责任
5、本网站图片,文字之类版权,本网站无法鉴别所上传图片或文字的知识版权,如果侵犯,请及时通知我们,本网站将在第一时间及时删除。
6、凡以任何方式登录本网站或直接、间接使用本网站资料者,视为自愿接受本网站声明的约束。
XueXi Design